Beweis (Charakterisierung r.a.):

Þ: Falls A leer ist, leistet die Funktion g mit g(i)= div für alle i das gewünschte. Falls A nicht leer ist, gibt es eine berechenbare Funktion f mit f(IN)=A. Def dann g durch g(i):=das kleinste j mit f(j)=i. Diese Funktion ist berechenbar, denn sie entspricht folgendem FD:

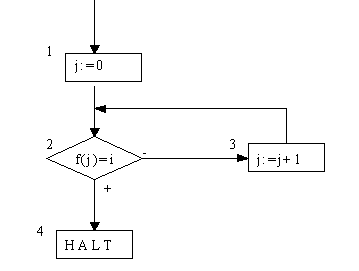
Es gilt dann: Falls iÎA, gibt es ein j mit f(j)=i, also gibt es ein minimales j mit f(j)=i, also ist g(i) def, also gilt iÎDef(g). Falls iÎA, gibt es kein j mit f(j)=i, also gibt es kein minimales j mit f(j)=i, also gilt g(i)=div, also gilt iÏDef(g).

Ü: Falls A leer ist, ist A nach Def r.a. Sei A nicht leer. Dann gibt es eine berechenbare Funktion g mit A=def(g) und ein n mit nÎA. Es gibt ferner eine rek. Funktion h mit h(i,t)=1, falls g(i) nach t Schritten einen Wert hat, sonst 0. Def. jetzt die Funktion f durch f(<i,t>):=i, falls h(i,t)=1, sonst n. f ist total und berechenbar.

Es gilt: Falls iÎA, hat g(i) einen Wert, also gibt es ein t mit h(i,t)=1, also gilt f(<i,t>)=i, also gilt iÎf(IN).

Falls iÏA, hat g(i) keinen Wert, also gibt es kein t mit h(i,t)=1, also gilt f(<i,t>)=n für alle t, also gilt iÏf(IN).

QED.

Übung 1: Beschreibe eine Registermaschine, die von zwei Zahlen das Minimum berechnet.

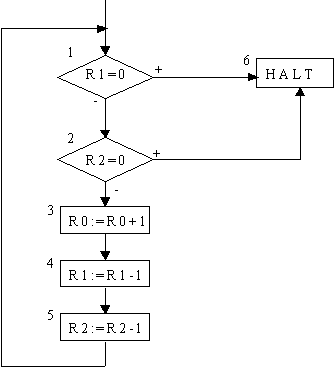
Beweis: Für die Schleife gilt: Falls x³n und y³n gilt ES⁵ⁿ(1,(a,x,y,0,...))=(1,(a+n,x-n,y-n,0,...)).

Beweis durch Induktion: Für n=0 gilt ES⁰(1,(a,x,y,0,...))=(1,(a,x,y,0,...))= (1,(a+0,x-0,y-0,0,...)).

Die Beh. Gelte für ein n und es gelte x³n+1 und y³n+1. Dann folgt ES⁵⁽ⁿ⁺¹⁾(1,(a,x,y,0,...))=

ES⁵ⁿ⁺⁵(1,(a+n,x-n,y-n,0,...))= ES⁵(1,(a+n,x-n,y-n,0,...))= ES⁴(2,(a+n,x-n,y-n,0,...)) = ES³(3,(a+n,x-n,y-n,0,...))

= ES²(4,(a+n+1,x-n,y-n,0,...)) = ES¹(5,(a+n+1,x-n-1,y-n,0,...)) = (1,(a+n+1,x-n-1,y-n-1,0,...)).

Falls x<y, gilt nun ES^x+1(1,(0,x,y,0,...))= ES¹(1,(x,0,y-x,0,...))= (6,(x,0,y-x,0,...)).

Falls y<x, gilt ES^y+2(1,(0,x,y,0,...))= ES²(1,(y,x-y,0,0,...))= (2,(y,x-y,0,0,...)) = (6,(y,x-y,0,0,...)).

Falls x=y, gilt ES^x+1(1,(0,x,y,0,...))= ES¹(1,(x,0,0,0,...))= (6,(x,0,0,0,...)).

Übung 2: Beschreibe eine Registermaschine, die von zwei Zahlen das Maximum berechnet.

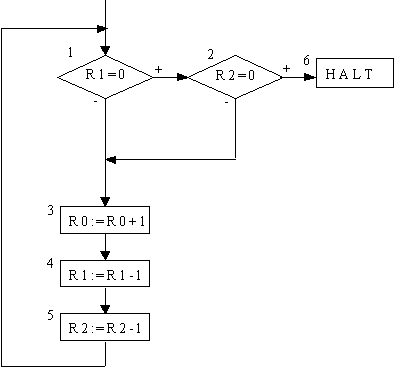
Beweis: Für die Schleife gilt: Falls x³n und y³n gilt ES⁵ⁿ(1,(a,x,y,0,...))=(1,(a+n,x-n,y-n,0,...)).

Beweis durch Induktion: Für n=0 gilt ES⁰(1,(a,x,y,0,...))=(1,(a,x,y,0,...))= (1,(a+0,x-0,y-0,0,...)).

Die Beh. Gelte für ein n und es gelte x³n+1 und y³n+1. Dann folgt ES⁵⁽ⁿ⁺¹⁾(1,(a,x,y,0,...))=

ES⁵ⁿ⁺⁵(1,(a+n,x-n,y-n,0,...))= ES⁵(1,(a+n,x-n,y-n,0,...))= ES⁴(2,(a+n,x-n,y-n,0,...)) = ES³(3,(a+n,x-n,y-n,0,...))

= ES²(4,(a+n+1,x-n,y-n,0,...)) = ES¹(5,(a+n+1,x-n-1,y-n,0,...)) = (1,(a+n+1,x-n-1,y-n-1,0,...)).

Falls x<y, gilt nun ES^x+1(1,(0,x,y,0,...))= ES¹(1,(x,0,y-x,0,...))= (6,(x,0,y-x,0,...)).

Falls y<x, gilt ES^y+2(1,(0,x,y,0,...))= ES²(1,(y,x-y,0,0,...))= (2,(y,x-y,0,0,...)) = (6,(y,x-y,0,0,...)).

Falls x=y, gilt ES^x+1(1,(0,x,y,0,...))= ES¹(1,(x,0,0,0,...))= (6,(x,0,0,0,...)).

Übung 3: Gebe ein FD für die Funktion Rest an mit Rest(a,b):=c, falls es ein n gibt mit n*b+c=a. Verfeinere das Flußdiagramm.

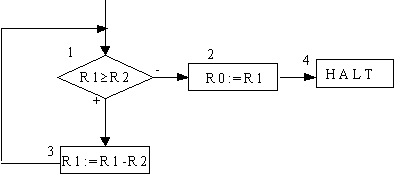
FD für R1:=R1-R2:

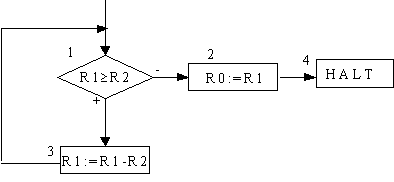
Verfeinerung:

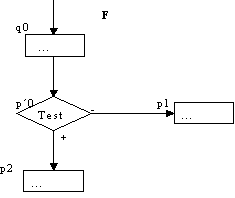
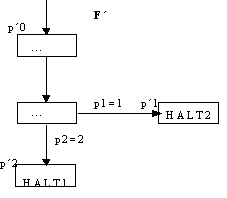
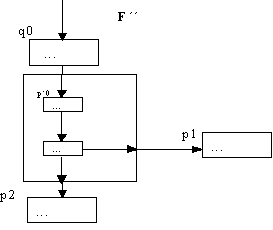
Beispiel:

Die Addition add ist primitiv-rekursiv. Def g durch g(x)= pr₁⁽¹⁾(x) und h durch h(x,y,z)= S(pr₃⁽³⁾(x,y,z)).

Dann gilt add(x,0)=g(x)=x und add(x,y+1)=h(x,y,add(x,y))=add(x,y)+1.

Beispiel:

Die Fakultät fak ist primitiv-rekursiv. Def g durch g()=S(0) und h durch h(y,z)= S(pr₂⁽³⁾(x,y,z)) * pr₃⁽³⁾(x,y,z).

Dann gilt fak(0)=g()=1 und fak(y+1)=h(y,fak(y))=(y+1)*fak(y).

Beispiel:

Die Fibonacci-Funktion ist primitiv-rekursiv. Sie wird def durch fib(0)=1, fib(1)=1 und fib(n+2)=fib(n)+fib(n+1).

Def g durch g()=1 und h durch h(y,z)=

Dann gilt f(0)=g()=1 unf f(1)=h(0,f(0))= h(0,1)=

und f(n+2)= h(n+1,f(n+1))= h(n+1, h(n,f(n)))