KE 1.............................................................................................................................................................................................. 2
1 Einleitung............................................................................................................................................................................. 2
2 Flußdiagramme und
Maschinen....................................................................................................................................... 2
3 Berechenbare
Zahlenfunktionen...................................................................................................................................... 4
KE 2.............................................................................................................................................................................................. 5
4 Transformationen von
Flußdiagrammen......................................................................................................................... 5
5 Berechenbare
Zahlenfunktionen II.................................................................................................................................. 5
KE 3.............................................................................................................................................................................................. 6
6 Turingmaschinen und
Bandmaschinen........................................................................................................................... 6
KE 4.............................................................................................................................................................................................. 7
7 Berechenbarkeit.................................................................................................................................................................. 7
KE 5.............................................................................................................................................................................................. 9
8 Die
Standardnumerierung j von P(1)................................................................................................................................ 9
KE 6............................................................................................................................................................................................ 11
9 Rekursive und
rekursiv-aufzählbare Mengen.............................................................................................................. 11
KE 7............................................................................................................................................................................................ 12
10 Berechenbarkeit auf
anderen Mengen........................................................................................................................ 12
KE 1
1 Einleitung
Def. (rekursiv): Eine Menge A heißt rekursiv, gdw. ihre charakteristische Funktion cfA berechenbar ist.
Sie ist def. durch cfA := 1, falls xÎA und 0 sonst.
Def. (r.a.): Eine Menge A heißt rekursiv aufzählbar, gdw. sie leer ist oder eine totale Funktion f existiert mit f(IN)=A.
Weitere Charakterisierung (r.a.): Eine Menge A heißt rekursiv aufzählbar, gdw. eine partielle Funktion f existiert mit Def(f) =A. (Beide Def sind gleichwertig)
Beweis (Charakterisierung r.a.)
2 Flußdiagramme und Maschinen
Def. (Flußdiagramm): F=(Q,D,s,q0,s,Qe)
Q Menge der Marken
D Datenmenge
s Funktion, die den Marken Funktionen und Tests und Ausgänge zuordnet
q0 Anfangsmarke
s Anzahl der Ausgänge
Qe Menge der Endmarken
Beispiel (Euklidischer Algorithmus):
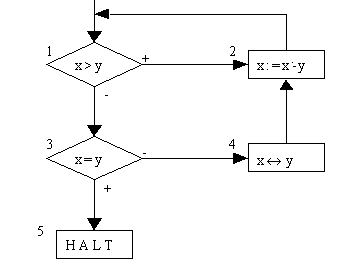
mit F=(Q,D,s,q0,s,Qe) und
Q = {1,2,3,4,5}
D = IN2
s(1)=(id, „x>y“, (2,3))
s(2)=(„x:=x-y“, 1, (1))
s(3)=(id, „x=y“, (5,4))
s(4)=(„x«y“, 1, (2))
s(5)=1
q0 = 1
s = 1
Qe = {5}
Def. (Semantik Flußdiagramm): Sei F=(Q,D,s,q0,s,Qe).
Menge der Konfigurationen KON:=Q´D.
Einzelschrittfunktion ES:Í KON ® KON.
Schrittzahlfunktion SZ:Í KON ® IN, SZ(q,d)=i, falls nach genau i Schritten eine Endkonfiguration erreicht wird.
Gesamtschrittfunktion GS:Í KON ® KON, liefert die Endkonfiguration oder div.
fF:Í D ® D mit fF(q0,d):=pr2(GS(q0,d)).
tF:Í D ® {1,...,s} mit tF(q0,d):=s(pr1(GS(q0,d))).
(fF, tF) heißt Semantik von F.
Def. (Maschinen): Eine Maschine ist def durch M=(F,X,Y,EC,AC).
F ist ein Flußdiagramm.
X ist eine Eingabemenge.
Y ist eine Ausgabemenge.
EC: X ® D ist die Eingabecodierung.
AC: D ® X ist die Ausgabecodierung.
Die Semantik ist def durch
fM: X ® Y mit fM:=AC°fF°EC und tM: X ® {1,...,s} mit tM:=tF°EC.
3 Berechenbare Zahlenfunktionen
Def. (Registermaschine): Eine Registermaschine ist eine Maschine M=(F,INk,IN,EC(k),AC) mit F=(Q,D,s,q0,s,Qe) und
D=ININ (Registerbelegungen)
EC(k):INk ® D, EC(k)(x1,x2,...,xk):=(0,x1,x2,...,xk,0,...)
AC(k):D ® IN, AC (a0,a1,...):= a0
Als Funktionen und Tests werden
nur „Ri:=Ri+1“, „Ri:=Ri![]() 1“ und „Ri=0“ verwendet.
1“ und „Ri=0“ verwendet.
Def. (Berechenbare Zahlenfunktionen):
1) Die Funktion f:Í INk ® IN heißt berechenbar, gdw es eine k-stellige Registermaschine M gibt mit f=fM.
2) Der Test t:Í INk ® {1,...,s} heißt berechenbar, gdw es eine k-stellige Registermaschine M mit s Ausgängen gibt mit t=tM.
Def. (verallgemeinerte Registermaschine): Eine verallgemeinerte Registermaschine ist eine Maschine M=(F,INk,IN,EC(k),AC) mit F=(Q,D,s,q0,s,Qe) und
D=ININ (Registerbelegungen)
EC(k):INk ® D, EC(k)(x1,x2,...,xk):=(0,x1,x2,...,xk,0,...)
AC(k):D ® IN, AC (a0,a1,...):= a0
Es wird entweder eine Funktion g auf ein Register und der triviale Test 1 mit einem Ausgang oder die identische Funktion id und ein Test mit zwei Ausgängen verwendet.
Satz: Wenn in einer verallgemeinerten Registermaschine alle Funktionen und Tests berechenbar sind, sind auch fM und tM berechenbar.
Übung 1: Beschreibe eine Registermaschine, die von zwei Zahlen das Minimum berechnet.
Übung 2: Beschreibe eine Registermaschine, die von zwei Zahlen das Maximum berechnet.
KE 2
4 Transformationen von Flußdiagrammen
Def. (Einsetzung): Seien F=(Q,D,s,q0,s,Qe) und F´=(Q´,D,s´,p´0,v,Q´e) Flußdiagramme.
F´ heißt an der Stelle p´0 in F einsetzbar, gdw QÇQ´= {p´0 } und f:ÍD ® D, t:ÍD ® {1,...,v} sowie p1,...,pv existieren mit s(p´0)=(f,t,(p1,...,pv)).
Sei F´´=(Q´´,D,s´´,q0,s,Q´´e) def durch
Q´´:=(QÈQ´)\Q´e
Q´´ e:= Qe
s´´(q):= s(q), falls qÎQ\{p´0}
s´´(q):= (f´,t´,(c(r1),..., c(ri))), falls qÎQ´\ Q´e und s´(q):= (f´,t´,(r1,..., ri)).
F´´ heißt dann def durch Einsetzung von F´ in F an der Stelle p´0.
Übung 3: Gebe ein FD für die Funktion Rest an mit Rest(a,b):=c, falls es ein n gibt mit n*b+c=a. Verfeinere das Flußdiagramm.
Satz (Verfeinerung):
Die Semantik eines Flußdiagramms ändert sich nicht durch Verfeinerung. Dabei muß das verfeinernde FD die gleiche Semantik haben wie der ersetzte Knoten.
Def. (Simulation): d Sim d´ heißt, daß d´d simuliert.
Es gilt f Sim f´, gdw (d Sim d´) Þ (f(d) Sim f(d´) oder f(d)=f(d´)=div).
Es gilt t Sim t´, gdw (d Sim d´) Þ (t(d) = t(d´) oder t(d)=t(d´)=div).
Satz (Simulation): Seien F=(Q,D,s,q0,s,Qe) und F´=(Q,D´,s´,q0,s,Qe) Flußdiagramme und gelte für jedes qÎQe s(q)=s´(q) und für jedes qÎQ\Qe (s(q)=(fq,tq,(p1,...,pk)) und s´(q)=(f´q,t´q,(p1,...,pk)) Þ fq Sim f´q und tq Sim t´q).
Dann gilt fF Sim fF´ und tF Sim tF´, also F´ simuliert F.
Satz (Simulation von Maschinen): Seien M=(F,X,Y,EC,AC) mit Datenmenge D und M´=([EA,H,AA],X,Y,EC´,AC´) mit Datenmenge D´ Maschinen mit D Sim D´. Falls
EC(x) Sim EA°EC´(x) für alle xÎX und
fF Sim fH und tF Sim tH und
AC(d)=AC´°AA(d´) für d Sim d´,
dann folgt fM Sim fM´und tM Sim tM´.
Übung 4: Simuliere mit einer Registermaschine die Addition und die Multiplikation von komplexen Zahlen. Die Relation Sim ist dabei gegeben durch x+i*y Sim (a,b) gdw. x=a und y=b.
Hinweis: (a+ib)+(x+iy)=((a+x)+i(b+y)) und (a+ib)*(x+iy)=ax+aiy+ibx+iiby=((ax-by)+i(ay+bx)).
5 Berechenbare Zahlenfunktionen II
Beweis des Satzes
über verallgemeinerte Registermaschinen
Def. (Cantorsche
Paarungsfunktion): p:IN2®IN
wird def durch p(x,y)= ![]() = ½(x+y)(x+y+1)+y.
= ½(x+y)(x+y+1)+y.
Def. (Cantorsche Tupelfunktionen): p(1)(x)=x. p(n+1)(x1,...,xn+1)= p(p(n)(x1,...,xn),xn+1).
Def:
P(k):= Menge der partiell rekursiven Funktionen f:ÍINk®IN.
R(k):= Menge der totalen rekursiven Funktionen f:INk®IN.
P:= Menge aller partiell rekursiven Funktionen.
R:= Menge aller totalen rekursiven Funktionen.
Def (primitive
Rekursion):
f:INk+1®IN sei def durch f(x,0)=g(x) und f(x,y+1)=h(x,y,f(x,y)) mit g:INk®IN und h:INk+2®IN. f=Prk(g,h) ist dann eindeutig def und entsteht durch primitive Rekursion.
Def (m-Rekursion):
Def mx[Q(x)]:=min M, falls M:={kÎIN | Q(k)}¹Æ, div sonst.
Es sei h:INk+1®IN.Dann sei m~(h):ÍINk®IN def durch m~(h)(x)= m y[h(x,y)=0]. m~(h) entsteht durch m-Rekursion.
Lemma:
Sei L eine k-stellige Registermaschine. Dann ist h:INk+1®IN mit
h(x,t)=1+fL(x), falls SZL(EC(x))=t, 0 sonst, berechenbar.
Beweisidee: Neues Register als Schrittzähler einbauen.
Anwendung:
Beweis der Äquivalenz der beiden Def der rekursiven Aufzählbarkeit.
Def (WHILE-Programme): Rek Def durch
Ri+ und Ri- sind WHILE-Programme
Mit P und Q sind auch (P;Q), (Ri | P | Q) und (Ri : P)
Def (Semantik der WHILE-Programme):
t(Ri+)(a0,a1,...):=( a0,a1,..., ai-1,ai+1, ai+1,...)
t(Ri-)(a0,a1,...):=(
a0,a1,..., ai-1,ai![]() 1, ai+1,...)
1, ai+1,...)
t(P;Q):= t(Q)°t(P)
t(Ri | P | Q)(d):= t(P), falls d(i)=0, sonst t(Q)
t(Ri : P)(d):= t(P)t(d), falls die Schleife t-mal durchlaufen wird, sonst div.
Satz:
Die Menge der WHILE-berechenbaren und der Register-berechenbaren Funktionen ist identisch.
Beweisidee:
KE 3
6 Turingmaschinen und Bandmaschinen
Def (Turingmaschine)
Def (berechenbare Wortfunktion): Eine Funktion f:Í(S*)k®S* heißt berechenbar, wenn sie durch eine Turingmaschine berechnet wird.
Satz: Zu einer
Register-berechenbaren Funktion f gibt es eine Turing-berechenbare Funktion f´
mit f´(0x1,...,0xk)=0f(x1,...,xk).
Beweisidee:
Das Register i wird auf dem i-ten Band simuliert.
Def (Bandmaschine):
Ist im wesentlichen eine Turingmaschine, die mit einem einzigen Band arbeitet.
Satz
(Turing-bb=Band-bb):
1) Zu jeder Bandmaschine gibt es eine Turingmaschine, die dieselbe Funktion berechnet.
2) Zu jeder Turingmaschine gibt es eine Bandmaschine, die dieselbe Funktion berechnet.
Beweisidee:
1) Simuliere das Band der Bandmaschine auf dem Band 0 der Turingmaschine und nehme eine Eingabeanpassung vor.
2) Simuliere alle Bänder der Turingmaschine auf dem einzigen Band der Bandmaschine. Vergrößere dazu das Bandalphabet so, daß jedes Zeichen jeweils die untereinanderstehenden Zeichen der m gebrauchten Bänder codiert und sogar, auf welchen Zeichen der Schreib-Lese-Kopf steht.
Satz (Hilfssymbole):
Zu jeder Bandmaschine gibt es eine äquivalente, die als Hilfssymbol nur B verwendet.
Beweisidee:
Kodiere die m Zeichen außer B durch Kombinationen gleicher Länge aus Symbolen von S mit élog(m)ù Zeichen. Ersetze alle Befehle auf einzelnen Zeichen durch Programme, die jeweils auf élog(m)ù Zeichen arbeiten.
KE 4
7 Berechenbarkeit
Def (Numerierung):
Eine Numerierung einer Menge M ist eine möglicherweise partielle surjektive Funktion n:ÍIN®M.
Jedes Element von M bekommt dadurch mindestens eine (evtl. auch mehrere) Nummern.
Def
(Standardnumerierung von S*):
Sei S ein Alphabet mit n:=card(S) und ai das i-te Zeichen für 1£i£n. Sei s:S*®IN def durch
s(e):=0 und s(aikaik-1...ai0):=iknk+ik-1nk-1+...+i1n+i0.
Dann heißt n: IN ® S* mit n:=s-1 eine Standardnumerierung von S*.
Satz:
Sei S ein Alphabet
und n:
IN ® S* eine Standardnumerierung von S*
und n´(i1,...,ik):=(n(i1),..., n(ik)). Für g:Í(S*)k® S* gilt dann: g
berechenbar Û
n-1gn´:ÍINk® IN
berechenbar.
Für f: ÍINk® IN gilt analog: f berechenbar Û nfn´-1: Í(S*)k® S* berechenbar.
Def (primitiv-rek
Funktionen):
Werden aus den Grundfunktionen Gr:={0,Z,S}È{pri(k) | 1£i£k} mit den Operatoren Sub und Prk in endlich vielen Schritten def, Bez PRK.
Satz:
An: IN® IN werden def durch
A0(x):= 1, falls x=0, 2, falls x=1 und x+2 sonst.
An+1(x):=Anx(1).
Dann sind alle An primitiv-rek.
Satz
(Ackermann-Funktion):
Die Ackermann-Funktionen A: IN2® IN und Ad: IN® IN mit A(n,x):=An(x) und Ad(x):= Ax(x) sind berechenbar, aber nicht primitiv-rek.
Def
(LOOP-Berechenbarkeit):
LOOP-Programme sind wie WHILE-Programme aufgebaut, nur steht die Anzahl der Schleifendurchläufe zu Anfang der Schleife fest.
Satz:
Die Menge der LOOP-berechenbaren Funktionen ist gleich der Menge der primitiv-rek Funktionen.
Weitere Def der
Berechenbarkeit:
Markov-Algorithmen, l-definierbare Funktionen, durch Gleichungssysteme definierbare Funktionen, m-rek Funktionen.
Def (m-rek
Funktionen):
Werden aus den Grundfunktionen Gr:={0,Z,S}È{pri(k) | 1£i£k} mit den Operatoren Sub, Prk und m~ in endlich vielen Schritten def.
Satz:
Die m-rek Funktionen sind genau die berechenbaren Zahlenfunktionen.
Beispiel:
Die Addition add ist primitiv-rekursiv.
Beispiel:
Die Fakultät fak ist primitiv-rekursiv.
Beispiel:
Die Fibonacci-Funktion ist primitiv-rekursiv. Sie wird def durch fib(0)=1, fib(1)=1 und fib(n+2)=fib(n)+fib(n+1).
Bemerkungen:
Ackermann fand heraus, daß nicht alle m-rek Funktionen primitiv-rek sind: er fand die sogenannte Ackermann-Funktion. Die m-rek Funktionen entsprechen den While-berechenbaren Funktionen. Die primitiv-rek Funktionen entsprechen den Funktionen, die mit For-Schleifen berechnet werden können, wobei der Endwert der Schleife in der Schleife nicht geändert werden darf.
CHURCHSCHE THESE:
Die Register-berechenbaren Funktionen sind genau die maschinell (im intuitiven Sinne) berechenbaren Zahlenfunktionen.
Beweis:
Þ: trivial.
Ü: prinzipiell nicht beweisbar.
Konstruktion einer
nicht berechenbaren Zahlenfunktion (DIAGONAL-BEWEIS):
Sei y(i) die vom i-ten WHILE-Programm definierte Zahlenfunktion.
Sei f def durch f(i):=1, falls y(i)(i)=0, sonst 0.
Dann gilt f¹y(i) für alle i, denn für jedes i gilt f(i) ¹y(i)(i).
Die Funktion f ist so definiert, daß sie sich in der Diagonalen der Tabelle von jeder Funktion y(i) unterscheidet, und zwar an der Stelle i, also mit dem Argument i.
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
... |
|
y(0) |
y(0)(0) |
|
|
|
|
|
|
|
|
y(1) |
|
y(1)(1) |
|
|
|
|
|
|
|
y(2) |
|
|
y(2)(2) |
|
|
|
|
|
|
y(3) |
|
|
|
y(3)(3) |
|
|
|
|
|
y(4) |
|
|
|
|
y(4)(4) |
|
|
|
|
y(5) |
|
|
|
|
|
y(5)(5) |
|
|
|
y(6) |
|
|
|
|
|
|
y(6)(6) |
|
|
... |
|
|
|
|
|
|
|
... |
KE 5
8 Die Standardnumerierung j von P(1)
Def
(Standardnumerierung j):
1) Es sei a:{1,...,8}®W definiert durch (a1,...,a8):=(1,B,(,),:,,,R,L) und nW die aus a abgeleitete Standardnumerierung von W*.
2) nP:IN®BP sei die Numerierung der Bandprogramme.
3) x:BM®P(1) sei def. durch x(M):=i-1 fM i mit i(i):=1i.
4) Dann ist j:IN®P(1) def. durch ji:= j(i):=x°nM°nP(i) die Standardnumerierung von P(1).
Def (Standardkomplexität F):
Es ist F:IN®IN def. durch Fi(x):= F(i)(x):=SZi(q0i,(e,B,1xB)) die Standardkomplexität zu j, wobei q0i die Anfangsmarke und SZi die Schrittzahlfunktion der Bandmaschine nM°nP(i) ist.
Lemma:
h:IN3®IN, def. durch h(i,n,t):= 1+ji(n), falls Fi(n)£t, 0 sonst, ist berechenbar.
Beweisidee:
Auf Band 1 wird das i-te Bandprogramm geschrieben, auf Band 2 das Argument n, auf Band 3 der Zähler t und auf Band 4 die Anfangsmarke. Dann simuliert das Programm das Programm auf Band 1, dekrementiert bei jedem Schritt den Zähler t und endet, wenn das Bandprogramm auf Band 1 beendet wird oder der Zähler t 0 wird.
Satz (utm-Theorem):
Die universelle Funktion uj:ÍIN2®IN, def. durch uj(i,x):= ji(x), ist berechenbar.
Das utm-Theorem besagt, daß man statt unterschiedlicher Turingmaschinen eine einzige verwenden kann, die man programmieren kann.
Beweisidee:
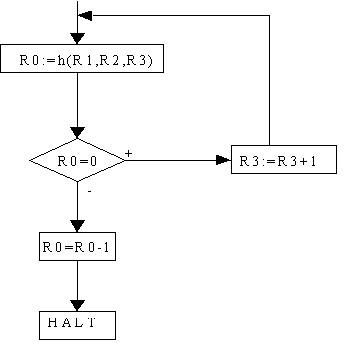
Satz (smn-Theorem, Übersetzungslemma):
Sei fÎP(2) berechenbar. Dann gibt es eine total-rek. Funktion rÎR(1) mit
("i,jÎIN) f(i,j)=jr(i)(j).
Man kann zu einer Turingmaschine mit zwei Argumenten eine neue schreiben, bei der das erste Argument nach der Eingabe auf das Band geschrieben wird.
Beweisidee:
Konstruiere eine Turingmaschine, die das erste Argument nach Start vor die Eingabe schreibt und dann weitermacht wie die ursprüngliche Maschine.
Satz (F-Theorem):
1) ("iÎIN) FiÎP(1).
2) ("iÎIN) Def(Fi)= Def(ji).
3) g:IN3®IN, def durch g(i,x,t):=1, falls Fi(x)£t, 0 sonst, ist berechenbar.
Beweisidee:
1) mit Rückgriff auf h.
2) trivial
3) mit Rückgriff auf h.
Satz
(Rekursionssatz):
Zu jeder Funktion fÎR(1) gibt es eine Zahl n mit jn=jf(n).
Beweisidee:
Zu v(z,x):=uj( uj(z,z),x) gibt es ein gÎR(1) mit jg(z)(x)= jjz(z)(x).
Zu w(i,x):=uj( i,g(x)) gibt es ein qÎR(1) mit jq(i)(x)= jig(x).
Mit h:=g°q gilt dann jjih(i)(x)= jjigq(i)(x) = jjq(i)q(i)(x) = jgq(i)(x) = jh(i)(x).
Wenn f=ji wähle n:=h(i).
Satz
(Selbstreproduktion):
Es gibt eine Zahl n, so daß jn(x)=n für alle xÎIN.
Beweisidee:
Def f durch f(i,x):=i. Dann gibt es ein rÎR(1) mit jr(i)(x)=f(i,x)=i. Nach dem Rekursionssatz gibt es eine Zahl n mit jn=jr(n). Es folgt jn(x)=jr(n) (x)=n für alle x.
Satz (Äquivalenzsatz
von Rogers):
Es sei y:IN®P(1) eine Numerierung von P(1). Dann sind folgende Eigenschaften äquivalent:
1) Es gibt „Übersetzer“ g,hÎR(1) mit j=y°g und y=j°h.
2) y erfüllt das utm-Theorem und das smn-Theorem.
Beweisidee:
Satz (smn-Theorem Û effektive Komposition):
Es sei y:IN®P(1) eine Numerierung von P(1), die das utm-Theorem erfüült Dann sind folgende Eigenschaften äquivalent:
1) y erfüllt das smn-Theorem.
2) Es gibt rÎR(2) mit yr(i,j)= yi ° yj.
ohne Beweis
Satz:
Es gibt keine totale surjektive Funktion y:IN®R(1) mit berechenbarer universeller Funktion.
Beweisidee:
Durch Diagonalisierung.
Frage:
Warum gilt dieser Satz nicht für j?
Satz:
Die berechenbare Funktion f:IN®IN mit f<i,x>:=uj(i,x) hat keine Fortsetzung in R(1).
Beweisidee:
Würde dem Satz davor widersprechen.
Satz (Halteproblem):
Es gibt keine Funktion hÎR(2) mit h(i,x)=1, falls ji(x) ex., 0 sonst.
Beweisidee:
Würde dem Satz davor widersprechen.
KE 6
9 Rekursive und rekursiv-aufzählbare Mengen
Def (rekursive
Menge):
Eine Menge AÍINk heißt rekursiv oder entscheidbar, gdw. die charakteristische Funktion cfA berechenbar ist. Sie ist def. durch cfA:INk®IN mit cfA(x):=1, falls xÎA, 0 sonst
Satz:
A ist rek. gdw. es eine totale berechenbare Funktion fÎR(k) gibt mit A=f-1{0}.
Satz:
Sei A unendlich. A ist rek. gdw. es eine wachsende (monotone) berechenbare Funktion fÎR(1) gibt mit A=Bild(f).
Beweisidee:
Satz
(Abschlußeigenschaften rekursiver Mengen):
1) Mit A1 und A2 sind auch INk\A1, A1ÈA2 und A1ÇA2 rekursiv.
2) Sei A rekursiv und fÎR(k). Dann ist f-1(A) rekursiv.
3) A rekursiv Û p(k)(A) rekursiv.
Def
(rekursiv-aufzählbare Menge):
Eine Menge AÍINk heißt rekursiv-aufzählbar (r.a.), gdw. es eine partielle berechenbare Funktion f gibtmit A=Def(A).
Satz
(Abschlußeigenschaften rekursiv-aufzählbarer Mengen):
1) Mit A1 und A2 sind auch A1ÈA2 und A1ÇA2 rekursiv.
2) Sei A r.a. und fÎP(k). Dann ist f-1(A) r.a.
3) A r.a. Û p(k)(A) r.a.
Satz
(Charakterisierung durch Bild, Projektionssatz):
1) A ist r.a. gdw. A=Æ oder A=Bild(g) für ein gÎR(1).
2) A ist r.a. gdw. A={x | ($t) (x,t)ÎB} für eine rek. Menge B.
3) A r.a. Û p(k)(A) r.a.
Satz:
A ist rek. gdw. A und INk\A r.a. sind.
Satz (Selbstanwendbarkeitsproblem):
Kj:={i | ji(i) existiert} ist r.a., aber nicht rek.
Beweisidee:
Satz (Halteproblem):
Kj0:={(i,x) | ji(x) existiert} ist r.a., aber nicht rek.
Beweisidee:
Def.
(Reduzierbarkeit):
A£B :Û es gibt ein fÎR(1) mit A=f-1(B).
Dies läßt sich auch ausdrücken durch die Bedingung xÎA Û f(x)ÎB für alle x.
Satz von Rice:
Falls FÎP(1) und F¹Æ und F¹P(1), dann ist die Menge j–1(F)={i | jiÎF} nicht rek.
Das heißt, daß nur die Nummernmengen der trivialen Teilmengen aller ber. Funktionen rek. sind.
Satz
(Korrektheitsproblem, Äquivalenzproblem):
Sei d def. durch d(i)=div für alle i.
1) Für jedes fÎP(1)\{d} sind die Mengen Mf:={i | ji =f} und IN\Mf={i | ji ¹f} nicht r.a.
2) Die Mengen {(i,j) | ji=jj} und {(i,j) | ji¹jj} sind nicht r.a.
Satz (Postsches
Korrespondenzproblem):
Satz:
1) Es gibt für jedes Beweissystem X Sätze der Form „1nÏKj“, die wahr, aber nicht beweisbar sind.
2) Man kann sogar mit einer berechenbaren Funktion zu einem beliebigen Beweissystem X die Nummer eines Satzes „1nÏKj“ berechnen, der wahr, aber nicht beweisbar ist.
KE 7
10 Berechenbarkeit auf anderen Mengen
Def. (Numerierung):
Eine Numerierung einer Menge M ist eine surjektive Abbildung n:ÍIN®M.
Def. einiger Standardnumerierungen.
Def.:
(n1,...,nk)-rekursive Mengen und (n1,...,nk)-rekursiv-aufzählbare Mengen.
Def.:
f:ÍIN®M heißt (n1,...,nk,n0)-berechenbar, gdw. es eine berechenbare Funktion g:ÍINk®IN gibt mit
f(n1(i1),...,nk(ik))= n0°g(i1,...,ik) für alle (n1(i1),...,nk(ik))Def(f).
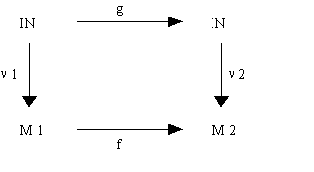
Def. (Reduzierbarkeit,
Äquivalenz):
1) n1£n2
2) n1ºn2
Satz von Rogers:
y erfüllt das smn-Theorem Û y³j .
y erfüllt das utm-Theorem Û y£j .
Def.:
Typ-II-Turing-Maschine und Darstellung. Cauchy-Darstellung der reellen Zahlen.
Satz:
Jede (r,...,r)-berechenbare Funktion f:ÍIRk®IR ist stetig.