Einführung

Def.: Phrasenstrukturgrammatik G=(V,S,P,S). Die Produktionen sind von der Form a -> b mit aÎV^*NV^* und bÎV^*.

Die Sprache zu einer Grammatik ist L(G). Für den Beweis von X=L(G) müssen zwei Richtungen bewiesen werden: XÍL(G) und L(G) ÍX.

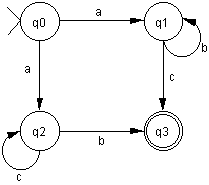
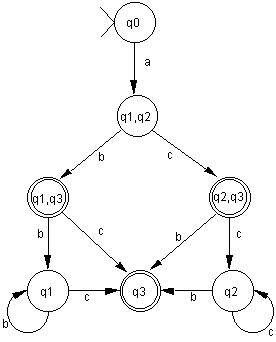
Beispiel für Umwandlung Transitionssystem in endlichen Automaten:

Das folgende Transitionssystem erkennt die Sprache

L={abⁱc | i≥0} È {acⁱb | i≥0}

Chomsky-Hierarchie

Sprache	Maschine	Grammatik	Beispiel
linear kontextfrei		linear kontextfrei	{a^ib^i}
regulär	endlicher Automat	linkslinear	{ab^*c}È{ac^*b}
regulär	endlicher Automat	rechtslinear	{ab^*c}È{ac^*b}

Reduzierung von Grammatiken:

Erst dafür sorgen, daß alle Nonterminale Strings erzeugen, dann erst unerreichbare Zeichen eliminieren!

Ein Beispiel dafür, daß man nicht umgekehrt verfahren darf:

S -> BC

B -> a

C -> C

Es sind alle Nonterminale erreichbar. Nur B erzeugt einen terminalen String. Also wäre die reduzierte Grammatik B->a. Das ist aber falsch.

Wenn man dagegen erst die unnutzen Zeichen eliminiert, bleibt B->a übrig. Da B nicht erreichbar ist, erhält man die leere Grammatik, was richtig ist.